Louis La Minh Hoang

Each book given away carries a message. We hope that it will give students more learning opportunities and hope for the future!

In this math lesson, I focused on complex inequalities through the use of specific and powerful inequality theorems, rather than trial-and-error or graphing alone. The emphasis was on recognizing structure and choosing the right theorem to simplify a difficult-looking problem.

A major part of the lesson involved applying classic results such as the AM–GM inequality (revision only), Cauchy–Schwarz inequality, and basic forms of Jensen’s inequality in algebraic settings. These theorems allowed complicated expressions to be bounded cleanly, turning messy inequalities into elegant arguments. Understanding the equality cases was especially important, since they often determined the exact conditions for maximum or minimum values.

We also worked with inequalities derived from completing the square and rearranging expressions into always-nonnegative forms. This approach made it possible to prove inequalities rigorously and to identify when an inequality holds for all real numbers versus only under certain constraints.

Some problems required combining multiple ideas, such as using AM–GM to estimate part of an expression and then refining the result with algebraic manipulation. Others involved symmetry, where recognizing interchangeable variables simplified the inequality significantly.

By the end of the lesson, complex inequalities felt less intimidating. With the right theorems and a clear strategy, even very difficult-looking inequalities became manageable. This lesson highlighted how inequality theory is not just about calculation, but about insight, structure, and mathematical elegance.

In this math lesson, I worked on integration, starting from the simple and foundational ideas before moving on to slightly more involved applications. The goal was to build a clear understanding of what integration actually represents, not just how to perform it mechanically.

We began with basic integrals of common functions, treating integration as the reverse process of differentiation. This helped connect new ideas with what I had already learned, making the rules feel more natural rather than memorized. Understanding how powers change and why constants appear in the result was an important part of this stage.

We also discussed the meaning of the constant of integration and why it must always be included when finding an indefinite integral. Instead of seeing it as an annoying extra symbol, we linked it to the idea that many different functions can have the same derivative.

Simple applications were introduced as well, especially interpreting integration as the area under a curve. Even at this basic level, it required careful thinking about limits and the shape of graphs, reinforcing the connection between algebra and geometry.

Although the content was introductory, this lesson laid the groundwork for more advanced integration techniques later on. By starting with simple cases and focusing on understanding, integration began to feel like a logical extension of differentiation rather than a completely new and separate topic.

In this math lesson, I revised the topic of similar triangles, focusing on understanding the reasoning behind similarity rather than just applying ratios mechanically. Although the concept is familiar, the problems showed how powerful and subtle similarity can be in geometry.

We reviewed the conditions for triangle similarity, and discussed how these guarantee that two triangles have the same shape even if their sizes are different. The emphasis was on recognizing similarity within complex diagrams, where the triangles are not immediately obvious and may be rotated, inverted, or partially overlapping.

Many of the questions required setting up correct proportional relationships between corresponding sides. Choosing the right ratios was critical, as one mistake could break the entire solution. Some problems involved combining similarity with parallel lines, midpoints, or intersecting transversals, which added an extra layer of difficulty.

We also used similar triangles to solve problems involving lengths, heights, and distances that could not be measured directly. These applications showed how similarity turns geometry into a powerful problem-solving tool rather than a purely theoretical idea.

Overall, this revision reinforced how similar triangles form a bridge between visual geometry and algebraic thinking. When used carefully, they allow complex geometric situations to be simplified into clean, logical relationships that are both elegant and effective.

In my math lesson, I focused on revising congruent triangles, reinforcing both the theory and the logical reasoning behind it. Even though this is a familiar topic, the revision showed that it is far more than just memorizing conditions — it is about building solid mathematical arguments.

We reviewed the main criteria for triangle congruence and discussed why each condition is sufficient to guarantee that two triangles are exactly the same in size and shape. Rather than treating these as rules to apply blindly, we examined how each condition restricts a triangle’s structure until only one possible shape remains.

The problems were more demanding than basic identification exercises. Many required multi-step proofs, where congruent triangles were used as an intermediate result to deduce further properties, such as equal angles, equal sides, or parallel lines. Choosing the correct pair of triangles to compare was often the hardest part of the problem.

We also practiced applying congruence in geometric constructions and diagrams with minimal information, where careful observation and logical deduction were essential. A small oversight in labeling or angle matching could lead to an incorrect conclusion, so precision mattered a lot.

By the end of the lesson, this revision strengthened my understanding of congruent triangles as a foundation of geometric reasoning. It reminded me that many complex geometry problems rely on these basic ideas, and mastering them makes advanced topics much clearer and more manageable.

In my computer science class, I studied databases and SQL, focusing on how data is stored, organized, and queried efficiently. Instead of seeing data as random information, this lesson emphasized structured thinking and logical design.

We began with the fundamentals of databases, learning why tables are used and how rows and columns represent records and fields. A key part of the lesson was understanding primary keys and how they uniquely identify each record, ensuring data integrity and preventing duplication. We also looked at how relationships between tables work, especially when linking data across multiple tables.

The main focus, however, was SQL (Structured Query Language). We practiced writing queries to retrieve specific data using commands such as Select, along with conditions to filter results. The challenge wasn’t memorizing syntax, but thinking clearly about what data was needed and how to express that request precisely in SQL.

We also explored how SQL can be used to sort data, limit results, and perform basic calculations. Some tasks required combining multiple conditions, which demanded careful logical reasoning to avoid errors or unintended results. These exercises showed how powerful SQL can be when used correctly, even with relatively simple commands.

Overall, this lesson made databases feel practical and essential. Learning SQL improved my ability to think systematically, break problems into smaller steps, and work with large sets of data efficiently — skills that are increasingly important in computer science and real-world applications.

In this physics lesson, I studied lenses at a deeper level, with a strong focus on formulas and problem-solving, especially situations where either the object or the lens itself is moving. Instead of just drawing ray diagrams, we analyzed how image position, size, and nature change dynamically.

We began by revising the key lens equations, particularly the lens formula and magnification relationships. These formulas became the main tools for predicting how an image behaves when the object distance changes. Rather than treating the formulas as isolated rules, we used them to understand trends — for example, how moving an object closer to a convex lens affects image distance and magnification, and why certain positions lead to virtual or real images.

The more challenging problems involved lenses in motion. In these questions, the object or lens was gradually moved, and we had to determine how fast the image moved in response or whether the image shifted in the same or opposite direction. Solving these required careful differentiation of the lens formula and a clear understanding of sign conventions, making the problems more mathematical and less visual.

We also studied cases where the image transitions between different states, such as from real to virtual, or from inverted to upright. Identifying these critical positions required both algebraic precision and physical intuition. Some problems combined multiple ideas, such as changing magnification while keeping certain quantities fixed, which forced us to think about constraints rather than just raw calculation.

By the end of the lesson, lenses felt far more dynamic than static. The formulas were no longer just tools for finding numbers; they became a way to describe continuous change. This lesson showed how powerful mathematical analysis can be in optics, especially when understanding how small movements lead to significant changes in the final image.

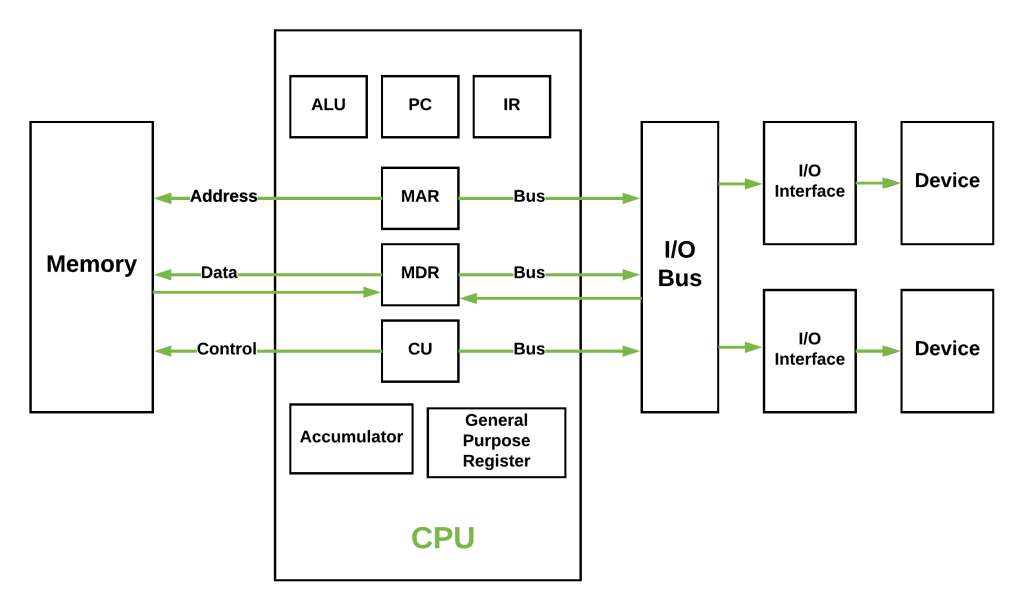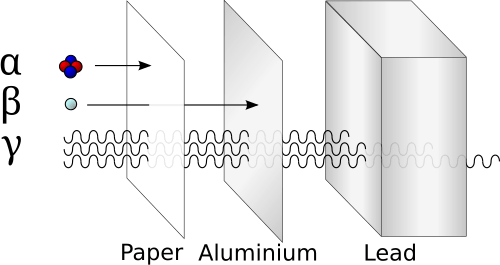
This physics lesson was a focused revision on radiation, but not in a shallow, definition-based way. Instead, it was about reconnecting all the concepts together and understanding how radiation behaves quantitatively and physically in real situations.

We revisited the three main types of radiation — alpha, beta, and gamma — but the emphasis was on comparing them through their properties, not just memorizing facts. We analyzed their ionising power, penetrating ability, and behavior in electric and magnetic fields, and more importantly, why those differences exist based on charge, mass, and energy.

A major part of the revision involved radioactive decay and half-life problems. These weren’t simple plug-in questions. We had to carefully track decay over multiple half-lives, interpret decay graphs, and reason backwards to find original quantities. Understanding the shape of decay curves and what each part of the graph represents was essential.

We also worked on radiation safety and applications, but again at a deeper level. Instead of listing uses, we justified why specific types of radiation are chosen for medical imaging, cancer treatment, smoke detectors, or industrial testing. Shielding wasn’t just “paper stops alpha” — it became a reasoning problem involving energy loss and interaction with matter.

Another challenging aspect was interpreting count-rate graphs and experimental setups. We had to distinguish background radiation from source radiation, analyze measurement errors, and explain fluctuations using statistical reasoning rather than calling them “mistakes.”

By the end of the lesson, this revision tied everything together — the theory, the graphs, the calculations, and the real-world meaning. Radiation stopped feeling like isolated facts and instead became a coherent system governed by probability, energy, and physical laws. Even as a revision lesson, it required careful thinking and strong conceptual understanding, proving that radiation is simple on the surface but deep underneath.

In my physics lesson, I revised the topic of variable resistors, but this wasn’t just about knowing what a rheostat or potentiometer is. The focus was on understanding how changing resistance affects an entire circuit and how to analyze problems logically rather than mechanically.

We reviewed how a variable resistor controls current and voltage in a circuit by changing the effective length of the resistive wire. Instead of memorizing results, we examined how this change influences the distribution of potential difference across components, especially when the variable resistor is connected in series or used as a potential divider.

The problems were more challenging than basic textbook ones. Some questions required predicting how the brightness of bulbs, readings on ammeters and voltmeters, or power dissipation would change as the slider moves. These problems demanded careful reasoning using Ohm’s law, the concept of equivalent resistance, and proportional relationships, rather than simply plugging numbers into formulas.

We also dealt with scenarios involving non-ideal components, such as voltmeters with internal resistance or variable resistors affecting multiple branches in a circuit. In these cases, drawing clear circuit diagrams and identifying which quantities stayed constant and which changed was crucial to reaching the correct conclusion.

By the end of the revision, I felt much more confident about variable resistors. They may seem simple at first, but when used in complex circuits, they become a powerful tool for testing understanding of electricity as a whole. This lesson reinforced how important logical thinking and clear analysis are in physics — even for topics that appear straightforward at first glance.